Triples of Orthogonal Latin and Youden Rectangles For Small Orders

Journal of Combinatorial Designs, Volume 27, Issue 4, p. 229-250, doi.org/10.1002/jcd.21642

Abstract

We have performed a complete enumeration of nonisotopic triples of mutually orthogonal 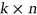Latin rectangles for 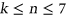. Here we will present a census of such triples, classified by various properties, including the order of the autotopism group of the triple. As part of this, we have also achieved the first enumeration of pairwise orthogonal triples of Youden rectangles. We have also studied orthogonal triples of 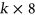rectangles which are formed by extending mutually orthogonal triples with nontrivial autotopisms one row at a time, and requiring that the autotopism group is nontrivial in each step. This class includes a triple coming from the projective plane of order 8. Here we find a remarkably symmetrical pair of triples of 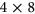rectangles, formed by juxtaposing two selected copies of complete sets of mutually orthogonal Latin squares of order 4.

Read more about the article: Triples of Orthogonal Latin and Youden Rectangles For Small Orders